
Scientific Committee: Shing Tung Yau, Jun Li, Bong Lian, Andrey Losev, Si Li, Sen Hu
Organizing Committee: Shing Tung Yau, Jun Li, Si Li, Bong Lian, Sen Hu, V. Lysov, Zou Hao, Ma Wenjie
Location: Room C108, Department of Physics , Jiangwan Campus, Fudan University (2005 Songhu Road, Yangpu District, Shanghai, China)
Zoom Meeting No.: 423 317 8953 (Password: SIMIS)
Topics to be covered:
. Matrix models and their large N limit
. Chiral Algebra
. AdS/CFT and gauge/gravity duality
. Spin chain and Calogero-Moser system
. Enumerative Geometry
. Fuzzy space and noncommutative geometry
Speakers:
| Alexander Ochirov | ShanghaiTech |
| Alexey Koshelev | ShanghaiTech |
| Andrey Losev | SIMIS |
| Ban Lin | YMSC, Tsinghua |
| Chi-Ming Chang | YMSC, Tsinghua |
| David Sauzin | Captial Normal University |
| Dongheng Ye | SIMIS |
| Hamed Adami | SIMIS |
| Ke-You Zeng | Perimeter Institute |
| Ling-Yan Hung | Tsinghua |
| Mauricio Romo | SIMIS |
| Minghao Wang | Boston University |
| Rui-Dong Zhu | Soochow University |
| Satoshi Nawata | Fudan University |
| Shanzhong Sun | Captial Normal University |
| Song He | Jilin University |
| Tomoki Nosaka | SIMIS |
| Yang Zhou | Fudan University |
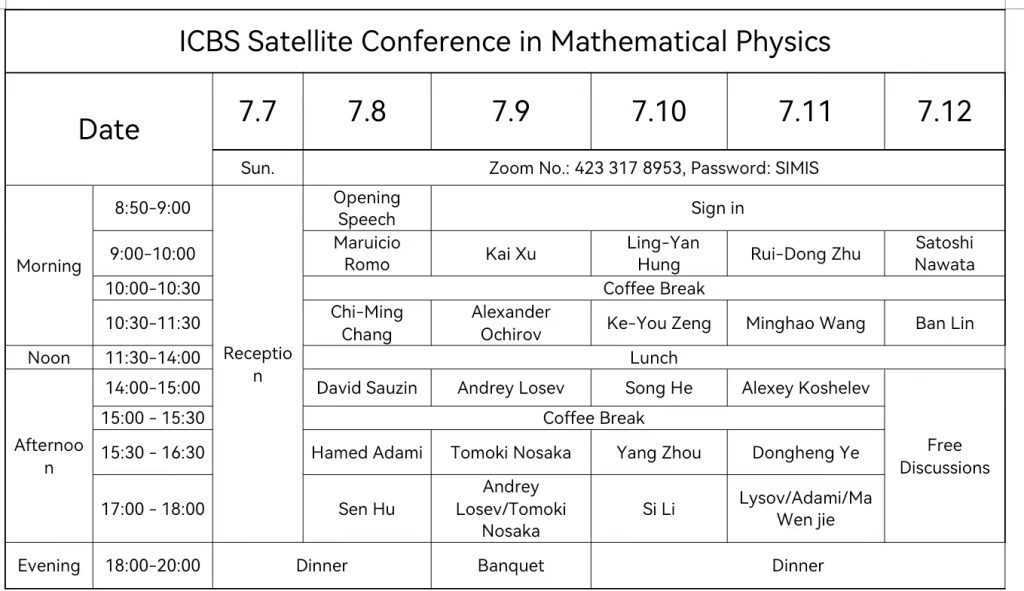
Titles and Abstracts
Alexander Ochirov
Title: Scattering amplitudes for QCD, gravity and massive particles
Abstract: I will discuss basic on-shell approach to scattering amplitudes. As an example, I will outline the derivation of two infinite families of tree-level scattering amplitudes in QCD involving a massive quark pair. Then I will generalize one of them to gauge theory coupled to massive particles of general spin. This will allow me to discuss a novel chiral-field approach to massive higher-spin theory and applications to classical gravitational dynamics of rotating black holes.
Andrey Losev
Title: Abstract for the discussion talk
Abstract: Compare two different approaches to QFT:Feynman approach that keeps structures of classical physics but changes geometry of the space-time and functorial approach that keeps the space-time classical but goes away from classical physics.I will show that functorial approach contains neither Plank constant nor the concept of fundamental field.Fields appear as derived notions. At the same time functorial approach has no ultraviolet divergences.The second half of my talk would be discussion with audience were I will answer questions concerning QFT.
Ban Lin(林般)
Title: Applications of B-brane transport in non-abelian GLSM
Abstract: The stringy Kahler moduli space of the IR theories of N=(2,2) gauged linear sigma model is constructed from the FI-theta parameter space, in where conical discriminant lie on the Coulomb vacua of the twisted multiples in gauge theory. The analytic continuation of B-brane central charges in this space is controlled by the “grade restriction rule” of hemisphere partition function of B-branes. We illustrate how to obtain this rule for anomalous and anomaly-free non-abelian GLSMs, and their applications on derived equivalences and the auto-equivalence of derived categories of coherent sheaves. Based on the joint work with M. Romo, J. Guo and H. Zou.
Chi-Ming Chang
Title: Supercharge Cohomology and Its Applications to Holography
Abstract: In this talk, I will introduce the notion of supercharge cohomology, which is semi-protected by supersymmetry and provides deeper insights beyond state counting. I will classify supercharge cohomologies in holographic conformal field theories into two categories: monotone (graviton) and fortuitous (black hole). By focusing on N=4 super-Yang-Mills theory, I will present explicit constructions of both monotone and fortuitous cohomologies and discuss their conjectural bulk duals as smooth horizonless geometries and black holes. Lastly, I will explore the spectrum of near-BPS operators and near-BPS black holes.
David Sauzin
Title: Resurgent transseries completions for partial theta series
Abstract: I will review our previous work with Li Han, Yong Li and Shanzhong Sun about the resurgence-summability aspects of partial theta series associated with arbitrary periodic sequences, and in particular the action of modular transformations on them. Here, the variable was confined to the upper half-plane, except for the quantum modularity phenomenon in which certain functions can be analytically continued to the right or to the left of an arbitrary rational point. Then I will explain recent developments concerning the functions of (z,\bar z) defined in the lower half-plane that appear naturally in that context: they enjoy similar quantum modularity relations and appear as a new kind of transseries completion. If time permits, I’ll outline the application to Gukov-Pei-Putrov-Vafa invariants and the proof of Witten’s asymptotic expansion conjecture for Witten-Reshetikhin-Turaev invariants for Seifert fibered homology spheres. The latter part is in collaboration with Han, Li, Sun, Jorgen Andersen and William Mistegard.
Dongheng Ye
Title: Chern-Simons matrix model and large N limit
Abstract: In this talk, we will talk about the algebra of quantum observables of the Chern-Simons matrix model which was originally proposed by Susskind and Polychronakos to describe electrons in fractional quantum Hall effects. We establish the commutation relations for its generators and study the large N limit of its representation. We show that the large N limit algebra is isomorphic to the uniform in N algebra studied by Costello, which is isomorphic to the deformed double current algebra studied by Guay. Under appropriate scaling limit, we show that the large N limit algebra degenerates to a Lie algebra which admits a surjective map to the affine Lie algebra of u(p). We conjecture that the large N limit algebra acts on the large N limit Hilbert space via the aforementioned degeneration limit, and we prove this conjecture in the p = 1 case by a detailed study of large N limit Hilbert space. This leads to a complete proof of the large N emergence of the u(p) model as proposed by Dorey, Tong and Turner in the case p = 1. This also suggests a rigorous derivation of edge excitation of a fractional quantum Hall droplet.
Hu sen
Title: Chern-Simons theory and its applications to condensed matter
Keyou Zeng
Title: Deligne Category and Large N Vertex Algebra
Abstract: The large N limit of gauge theory plays a crucial role in AdS/CFT duality and holography. Twisted holography offers a simplified approach to holography, in which we consider the large N limit of vertex algebras as toy model for gauge theories. In this work, we rigorously define these large N vertex algebras using the Deligne category. To achieve this, we first establish the notion of vertex algebras in a more general categorical context, which turns out to be an interesting concept on its own. Additionally, we discuss some of the applications of this framework.
Ling-Yan Hung
Title: Building Up Quantum Spacetimes with BCFT Legos
Abstract: Is it possible to read off the quantum gravity dual of a CFT directly from its operator algebra?
In this talk, I will present a step-by-step recipe for building up 3D quantum spacetimes dual to 2D CFTs, synthesizing results and techniques from conformal bootstrap, topological symmetries, real-space tensor network renormalization,
and the asymptotics of quantum 6j symbols. Quantum Liouville theory serves as a simple and explicit example,
illustrating how the exact CFT/gravitational path integral can be built up from triangulation and local pieces of BCFT correlation functions, which we call the “BCFT Legos”. This is essentially a tensor network that admits an interpretation of a state-sum of a 3D topological theory constructed with quantum 6j symbols of Uq(SL(2,R)) with non-trivial boundary conditions, and it reduces to a sum over 3D geometries weighted by the Einstein-Hilbert action to leading order in large c. The triangulation coincides with producing a network of geodesics in the AdS bulk, which can be changed making use of the pentagon identity and orthogonality condition satisfied by the 6j symbols, and arranged into a precise holographic tensor network. The constructive map between gravity and CFT naturally and explicitly bridges local geometrical data, algebraic structures, and quantum entanglement.
Mauricio Romo
Title: Quantum Trace and Length Conjecture
Abstract: I will review some aspects of the relation between a variant of the volume conjecture for hyperbolic 3-manifolds, the ‘length conjecture’ and its relation with complex Chern-Simons Theory, the quantum trace map, and M-theory.
Minghao Wang(王明浩)
Title: Factorization algebras from topological-holomorphic field theories
Abstract: Factorization algebras were originally proposed by Beilinson and Drinfel’d as a reformulation of Chiral algebras. This concept has been further developed by Costello and Gwilliam to capture operator product expansion in general quantum field theories. In this talk, I will construct factorization algebras by constructing perturbative quantization of topological-holomorphic field theories. In particular, I will show all the Feynman graph integrals of topological-holomorphic theories on flat spaces are ultraviolet finite, and certain anomaly-vanishing results hold. As an example, we obtain another proof of the existence of quantum 4d Chern-Simons theory. This is a joint work with Brian Williams.
Rui-Dong Zhu(朱睿东)
Title: A Topological Vertex for Orientifolds and Freezing
Abstract: The topological vertex formalism provides an alternative way to calculate Nekrasov instanton partition functions for theories with brane construction, and is deeply related to the integrability nature of the gauge theory. It has been extended to include O5-orientifolds in recent years. In this talk, we propose a new topological vertex formalism for O7^+-plane. Based on a mathematical identity, we show its consistency with O5-construction, which further uncovers a quantitative description of the freezing of O7^+/O6^+ in the string theory.
Satoshi Nawata
Title: 2d dualities from 4ds
Abstract: We unveil large classes of dualities among 2d supersymmetric gauge theories by compactifying 4D supersymmetric theories on S^2 with a topological twist. These 2d theories encompass N=(0,2), (2,2) and (0,4) supersymmetric theories. In this talk, I will present numerous open problems, puzzles, and future directions that I am currently exploring. This talk is based on joint work with Y. Pan and J. Zheng [arXiv:2310.07965] and a couple of ongoing works with W. Cui and my students (J. Huang, Z. Huang, J. Jiang, J. Zheng, S. Zhuang).
Si Li(李思)
Title: Quantization: Algebraic and Geometric Structures and Applications
Abstract:We discuss basic ideas on algebraic and geometric structures arising from quantization problem. We illustrate some applications in noncommutative geometry, mirror symmetry and topological string.
Song HE
Title: Holographic Correlators in Euclidean AdS3 and AdS Planar Black Holes
Abstract: In this talk, we present holographic stress tensor correlators on general Riemann surfaces, extending beyond torus cases to higher genus conformal field theories (CFTs) within the AdS/CFT correspondence framework.
We use the Schottky uniformization technique to address handlebody solutions for higher genus surfaces. We derive four-point stress tensor correlators and recurrence relations for higher-point correlators within the AdS3/CFT2 context. Additionally, we show holographic Euclidean thermal correlators of the stress tensor and U(1) current from the AdS planar black hole.
We set up perturbative boundary value problems for Einstein’s gravity and Maxwell theory, with gauge fixing and regularity conditions at the black hole horizon. The linearized Einstein and Maxwell equations relate to the Heun equation with degenerate local monodromy. Using the connection relation of local solutions of the Heun equation, we obtain exact two-point thermal correlators for the U(1) current and stress tensor in the scalar and shear channels.
Tomoki Nosaka
Title: Large N expansion of superconformal indices of M2-branes
Abstract: In the theories of multiple M2-branes, there are heavy (D ~ N: number of M2-branes) operators which correspond to wrapped M5-branes under the AdS/CFT correspondence, and to reveal such effects from M2, M5 and gravity perspective is one of hot topics in theoretical high energy physics. Recently we found an exact large N expansion for a superconformal index of N M2-branes on different orbifold backgrounds, including the exact form of the effects of wrapped M5-branes. The results are consistent with the known exact forms of the superconformal indices of m M5-branes for m = 1 and infinity. We also found that the Fermi gas formalism, the method we used to solve the superconformal index, is a powerful tool for the indices with insertion of Wilson lines as well.
Xu Kai
Title: Moduli of principal bundles on curve and semiorthogonal decomposition
Abstract: In this talk we construct semiorthogonal decompositions of moduli of (twisted) principal bundles on a curve into its symmetric powers. The essential ingredients in the proof include Borel-Weil-Bott theory for loop groups, Weyl modules of current groups and Kac-Moody localization of D-modules. We also discuss its relationship with four-dimensional gauge theory.

Shanghai Institute for Mathematics and Interdisciplinary Sciences
